
■ 목차
1. 함수 설명
2. 표준편차 - 통계의 기본 이해
3. Stdev 함수의 구문 / 사용방법
4. Stdev 함수 사용해 보기 - 표준편차 구하기
** 핵심 요약
- 엑셀에서 표준편차(Stadard deviation)를 구해주는 Stdev 함수가 있습니다.
- 평균에서 벗어나는 산포 정도를 알 수 있는 대표적인 통계함수이며 평균, 최소, 최대와 함께 가장 많이 사용이 되는 통계 데이터입니다.
- 표준편차가 통계적으로 어떤 의미인지 모집단, 표본집단이 어떻게 다르며 그래서 나는 어떤 함수를 사용해야 하는지 알아보도록 하겠습니다.
- 통계가 어렵지 Stdev 함수를 사용하는 것을 그렇게 어려운 부분이 없습니다.
1. 함수 설명
- 엑셀에서 통계함수 Stdev 함수는 표준편차, Standard deviation을 구해주는 함수입니다.
- 데이터 값들이 평균에서 벗어나는 정도를 표현해 주는 통계 함수로 분산(Variance)의 제곱근으로 구할 수 있습니다.
- 수식으로는 = (Sum (x - avg) ^2 / n )^0.5으로 표현이 가능하며
- 데이터 집합을 분석하는 경우에 반드시 사용하는 함수입니다.
- 데이터 분석을 하게 되면 기본적으로 사용하는 함수로 평균 (Average 함수), 최대 (Max 함수), 최소 (Min 함수), 데이터 개수 (Count a 함수)
- 그리고 계산 값으로 R 값 (Range, 최대 - 최소), 변동 계수라고 C.V (Coefficient of variation = Stdev / Average) 정도가 있습니다.
- Average 함수가 평균을 보는 것이라면 Stdev 함수는 데이터가 산포 즉 얼마나 평균이나 중앙값을 기준으로 흩어져 있는지를 측정하는 통계 데이터입니다.
- 그리고 평균의 크기가 다른 경우에 산포의 정도를 비교하기 위해서 변동 계수 (C.V %)를 구해서 상대 비교를 하곤 합니다.
- 통계적인 의미를 어느 정도 이해를 해야 값을 구하고 데이터 집단에 대한 평가를 할 수 있기 때문에 필요한 부분이고
- 엑셀 함수의 사용법 자체는 그렇게 어렵지 않기 때문에 편하게 사용을 하시면 됩니다.
- 주의하실 점은 모집단의 표준편차 함수 (Stdevp 함수)와 표본 집단의 표준편차 함수 (Stdev 함수)가 구분되고 결과 값도 조금 다르기 때문에
- 어떤 함수를 사용해야 하는지 그리고 대상이 되는 데이터가 모두 "숫자" 이기 때문에 숫자가 아닌 데이터는 어떻게 되는지 정도 이해를 하시고 주의해서 사용을 하시면 됩니다.
2. 표준편차 - 통계의 기본 이해
- 사실 저는 통계를 전공한 사람은 아닙니다.
- 실무적으로 데이터를 분석할 일들이 많기 때문에 통계에 관심을 가지고 있기는 하지만 제가 이해하는 수준이고
- 이런저런 통계적인 개념이 있다고 같이 이해를 해주시면 될 것 같습니다.
- 1) 표준편차 (Standard Deviation) : 평균에서 벗어난 정도
- 통계적인 개념에 대해서 지식이 있으시거나 모집단, 표본집단의 표준편차를 구분하여 사용이 가능하신 경우는 본 내용은 그냥 넘어가셔도 됩니다. ^^
- 데이터가 평균 혹은 중앙값에서 평균적으로 얼마나 떨어져서 있는지를 구하는 통계값입니다.
- 표준편차가 크다는 얘기는 평균은 70점이지만 40점도 있고 100점도 있고 이렇게 평균에서 많이 떨어진 값들이 있고
- 결국 실력이 들쑥날쑥하고 편차가 크다는 의미입니다. 좋은 실력은 아닌 것 같네요 ^^
- 그래서 항상 이런 표준편차의 값을 구하고 어느 집단의 성적이 혹은 물성이 균일하게 잘 나오는지를 비교합니다.
- 먼저 "평균"이 있고 평균에서 벗어나는 정도가 "편차(x - average)"입니다.
- 그런데 편차를 모두 합계를 하게 되면 +/-가 되어 0 이 되어 버립니다.
- 그래서 편차를 양수로 만들기 위해서 제곱 ( (x - average)^2 )를 하고 이의 합계를 구하여 데이터의 개수 (n)으로 나누어 주게 되면 "분산(Deviatio)"의 공식이 됩니다.
- "편차" : 평균과의 차이값
- "분산" : 편차 제곱의 합
- "표준 편차" : 분산의 제곱근

- "분산"도 평균에서 벗어나는 정도를 나타내는 통계 수치이지만 제곱을 해서 그런지 데이터의 크기가 큽니다.
- 그래서 "표준 편차"는 "분산"을 제곱근하여 "평균에서 벗어난 정도"를 적당한 크기로 만들어서 사용하게 되고 표준편차의 공식은 아래와 같습니다.

- 평균에서 벗어난 정도의 합계를 구하기 위해서 제곱을 했다가 숫자가 너무 커지니깐. 다시 제곱근을 해준 모양새입니다.
- 2) 표준편차 : 모집단의 표준편차, 표본 집단의 표준편차
- 다음은 개념은 명확하지만 항상 함수 사용 시에 조금 혼돈이 되는 개념이 나옵니다.
- 바로 "모집단"과 "표본 집단"입니다.
- "모집단"이란 한문으로는 어미 모 (母), 영어로는 Population (전체 인구)라는 뜻을 가진 단어로
- 우리가 분산이나 표준편차를 알고 싶어 하는 전체대상을 의미합니다.
- 반면에 "표본집단"이라고 하면 영어로 Sample로 전체 데이터를 모르거나 알기 힘든 경우의 부분에 해당하는 데이터 집합을 의미합니다.
- 대한민국 국민의 평균 키를 알고 싶다면 모집단은 "대한민국 인구 전체"를 의미하며
- 대한민국 국민의 평균 키라는 값은 진실된 값이 이상적으로 존재하지만 다만 우리는 실무적으로 알 방법이 없는 것이 특징입니다.
- 이렇듯이 보통의 "모집단"이라고 하면 현실의 벽에 부딪혀서 알 수 없는 값이고
- 거의 대부분의 집합의 데이터는 "표본 집단" 즉 전체 집단에서의 Sample로 된 일부의 데이터를 의미합니다.
- 그렇다고 항상 모르는 것은 아닙니다. 우리가 알고자 하는 범위가 작은 경우는 충분히 알 수 있는데
- 만약 우리 반 학생의 중간고사 평균 및 편차를 구하고 싶다면 충분히 알 수가 있는 경우입니다.
- 이렇게 모집단인 경우의 분산, 표준편차의 경우 데이터 개수 n으로 나누기를 해주는 공식을 사용지만
- 거의 대부분은 진실된 전체 집합을 잘 모르겠다이고 이런 경우는 "표본 집단(Sample)"의 표준편차를 구하게 되고
- 전체 데이터 개수를 하나 줄여서 n-1로 나누어주는 공식을 사용해서 구하게 됩니다.
- 그래서 데이터의 개수가 어마어마하게 많아지면 n = n-1이 되어 2개의 수식이 같아지게 됩니다.
- 그리고 보통의 경우 표본집단의 분산, 표준편차가 n-1로 나누어 주기 때문에 조금 큰 값을 가지게 됩니다.

- 이를 엑셀 함수에 적용을 하게 되면
- 모집단(Population)의 표준편차 : Stdev.P 함수 (Stdevp 함수 - 엑셀 2007 이전 버전의 함수임)
- 표본 집단 (Sample)의 표준편차 : Stdev.S 함수 (Stdev 함수 - 엑셀 2007 이전 버전의 함수임)
- 그냥 잘 모르겠다 → "표본 집단의 표준 편차"를 사용하시면 됩니다. ^^
- 같은 함수로 2가지가 존재하며 가능한 최신 버전인 Stdev.P, Stdev.S 함수를 사용해 주시기 바랍니다.
3. Stdev 함수의 구문 / 사용방법
- 아래 구문은 엑셀 도움말의 설명 내용입니다. 우리는 엑셀 함수의 구문을 다 외울 수도 없고 그럴 필요도 없습니다.
- 다만 엑셀 도움말과 함수사용 시 표시되는 풍선도움말의 용어들에 익숙해질 필요가 있기 때문에 기회가 될 때마다 편하게 봐주시기 바랍니다.
- STDEV(number1, [number2],...)
- number1 필수 요소입니다. 모집단 표본에 해당하는 첫 번째 숫자 인수입니다.
- number2,... 선택 요소입니다. 모집단 표본에 해당하는 숫자 인수로, 2개에서 255개까지 지정할 수 있습니다.
- number1, 인수로는 number 즉 "숫자"가 들어갑니다. 보통은 숫자가 들어가 있는 셀 참조 주소를 지정해 주어 사용을 합니다.
- 특히 주의를 해주실 부분은 바로 "숫자"입니다. 숫자가 아닌 것들로 문자, 논리값(True, False) 그리고 숫자처럼 보이는 문자가 있습니다.
- 엑셀에서 분산, 표준편차 등의 함수를 사용하실 때는 숫자여부를 포함하여 아래 부분정도 주의를 해주시고 사용을 해주시면 됩니다.
- 물론 내가 사용하고 있는 통계 함수의 통계적인 의미는 알고 계셔야 결과 데이터를 효율적으로 활용이 가능하겠지요. ^^
- ① 모집단, 표본집단의 어느 함수를 사용할 것인가? - 거의 대부분은 표본집단이다 (Stdev.S 함수 혹은 Stdev 함수 사용)
- ② 논리값, 문자형식의 데이터가 있다면 반드시 숫자로 변형 후 계산을 해주자. - 모두 무시된다.
- 논리값, 문자의 경우 "셀 참조 형식"으로 입력된 때랑 "직접 인수 값으로 입력 ( =STDEV.S(10,20,30) )" 할 경우가 다르기는 하지만
- 현실적으로 데이터를 하나하나 직접 인수로 입력하는 경우는 없기 때문에 그냥 결과적으로 모두 무시한다고 이해를 하시면 됩니다.
- Stdev, Stdevp, Stdev.S, Stdev.P 함수는 조금씩 다르지만 모두 같은 방식으로 사용을 하시면 됩니다.
4. Stdev 함수 사용해 보기 - 표준편차 구하기
- 다음 학급반 성적에 대한 표준편차를 구해보도록 하겠습니다.
- Stdev 함수는 Stdev.S 함수와 동일한 함수이며 표본집단 ( = Sample, 샘플 집단)에 대한 표준편차를 구해주는 함수입니다.
- 가능한 Stdev 함수대신에 Stdev.S 함수를 사용해 주시기 바랍니다.
- 사용방법은 Sum, Average 함수 등과 동일하게 함수를 입력하고 셀 참조 주소를 마우스로 지정해서 등록해 주시면 됩니다.
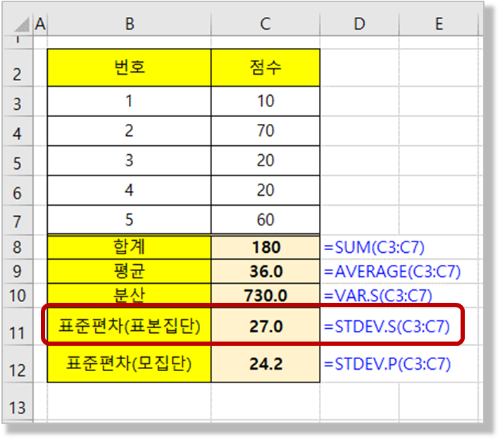
- 조금 억지 같지만 굳이 결과 값을 해석해 본다면 (5명이 한 반의 모든 인원이라고 한다면)
- 이 반의 진실된 표준편차는 = 모집단의 표준편차 = 24.2의 값을 가집니다.
- 그러면 이 반의 성적이 전체 학년의 성적에서 본다면 하나의 Sample군에 해당하기 때문에
- 우리는 전체 학생의 표준편차를 추정할 수 있으면
- 전체 학생의 표준편차 = 표본 집단의 표준편차 = 27.0로 추정이 가능합니다.
- 두 경우 모두 "전체의 표준편차"를 알고 싶은 경우이고 가지고 있는 데이터가 모집단인지 표본집단인지에 따라서 사용해 주는 공식을 다르게 사용해 주는 방식입니다.
- 이 경우 하나는 "전체 = 반, 데이터 = 반 = 모집단"이고 나머지 하나는 "전체 = 학급, 데이터 = 반 = 표본집단"이 되겠습니다.
- 이제 구분이 좀 가시는지요? 이렇듯이 사실 통계가 어렵지 엑셀 함수는 별거 없습니다. ^^
** 핵심 요약 : Stdev 함수 사용법 - 표준편차를 구해보자(Stdevp, Stdev.S, Stdev.P 함수)
1. 함수 설명
- 엑셀에서 통계함수 Stdev 함수는 표준편차, Standard deviation을 구해주는 함수이다.
- 수식으로는 = (Sum (x - avg) ^2 / n )^0.5으로 표현이 가능하며
- Stdev 함수는 데이터의 산포 즉 얼마나 평균이나 중앙값을 기준으로 흩어져 있는지를 측정하는 통계 데이터이다.
2. 표준편차 - 통계의 기본 이해
- 1) 표준편차 (Standard Deviation) : 평균에서 벗어난 정도
- 표준편차가 크다는 얘기는 각각의 데이터가 평균, 즉 중앙값에서 벗어나는 정도가 크다는 의미이다.
- "편차" : 평균과의 차이값
- "분산" : 편차 제곱의 합
- "표준 편차" : 분산의 제곱근
- 2) 표준편차 : 모집단의 표준편차, 표본 집단의 표준편차
- "모집단"이란 한문으로는 어미 모 (母), 영어로는 Population (전체 인구)라는 뜻을 가진 단어로 알고 싶은 전체 대상을 의미한다.
- "표본집단"이란 영어로는 Sample로 전체 데이터를 모르거나 알기 힘든 경우의 일부의 데이터, 부분을 의미한다.
- 모집단(Population)의 표준편차 : Stdev.P 함수 (Stdevp 함수 - 엑셀 2007 이전 버전의 함수임)
- 표본 집단 (Sample)의 표준편차 : Stdev.S 함수 (Stdev 함수 - 엑셀 2007 이전 버전의 함수임)
- 그냥 잘 모르겠다 → "표본 집단의 표준 편차"를 사용하면 된다.
3. Stdev 함수의 구문 / 사용방법
- STDEV(number1, [number2],...)
- number1 필수 요소입니다. 모집단 표본에 해당하는 첫 번째 숫자 인수입니다.
- number2,... 선택 요소입니다. 모집단 표본에 해당하는 숫자 인수로, 2개에서 255개까지 지정할 수 있습니다.
- number1, 인수로는 number 즉 "숫자"가 들어간다. 보통은 숫자가 들어가 있는 셀 참조 주소를 지정해 주어 사용한다.
- ① 모집단, 표본집단의 어느 함수를 사용할 것인가? - 거의 대부분은 표본집단이다 (Stdev.S 함수 혹은 Stdev 함수 사용)
- ② 논리값, 문자형식의 데이터가 있다면 반드시 숫자로 변형 후 계산을 해주자. - 모두 무시된다.
- Stdev, Stdevp, Stdev.S, Stdev.P 함수는 조금씩 다르지만 모두 같은 방식으로 사용하면 된다.
4. Stdev 함수 사용해 보기 - 표준편차 구하기
- Stdev 함수는 Stdev.S 함수와 동일한 함수이며 표본집단 ( = Sample, 샘플 집단)에 대한 표준편차를 구해주는 함수이다.
- 사용방법은 Sum, Average 함수 등과 동일하게 함수를 입력하고 셀 참조 주소를 마우스로 지정해서 등록해 주면 된다.
- 수식 : =STDEV.S(C3:C7)
[엑셀 함수 강좌-플러스] - 999. 엑셀 함수 Plus 목차
999. 엑셀 함수 Plus 목차
[엑셀 함수 강좌-플러스] - 001. (엑셀 함수 Plus) Text 함수 사용법 - 원하는 서식(포맷, 날짜/시간, 소수점, 퍼센트, 시간, 요일)을 텍스로 만들어 보자 [엑셀 함수 강좌-플러스] - 002. (엑셀 함수 Plus) Tr
nextmeok.tistory.com
* 엑셀 관련 궁금하신 거나 어려운 점이 있으시면 자유롭게 질문을 해주세요.
* 가능한 도움을 드릴 수 있도록 하겠습니다.
* 저도 많이 알지는 못하지만 누구나 그렇듯 시작이란 게 있고 경험이란 게 다를 것 같습니다.
* 편하게 문의하시면 됩니다. 저도 모를 수 있다. 감안해 주시고.
- ILU, SH -




댓글